pid 제어는 원하는 값에 도달하기 위한 기초적인 자동 피드백 제어 방법 중 하나입니다.
pid제어를 위해서는 몇가지 요소에 대한 정의가 필요합니다.
e(t) : 오차값이라 부르고, 목표값에서 현재값을 뺀 값입니다.
MV(t) : 제어량이라 부르고, 현재값에서 목표값에 도달하기 위해 제어기에 줄 값을 의미합니다.
알고리즘은 다음과 같습니다.
MV(t) = Kp*e(t)+Ki*(integral)e(t)+Kd*(derivative)*e(t)
PID제어는 사실 위키백과에 생각보다 설명이 잘 되어 있어 놀랐습니다.
문서에서 괜찮은 그래프가 있길래 하나 가져와봤습니다.
PID에 대한 내용은 이거 하나만으로 모두 정리될 것 같네요.
그래프를 참조하면서 읽으시면 도움이 크게 됩니다.
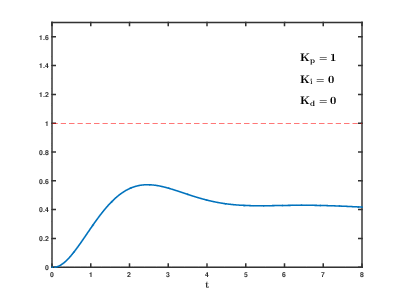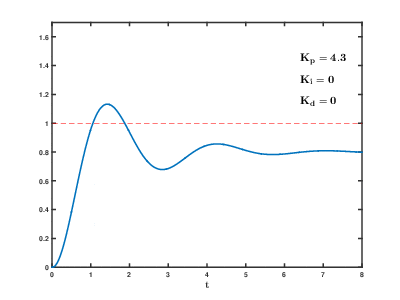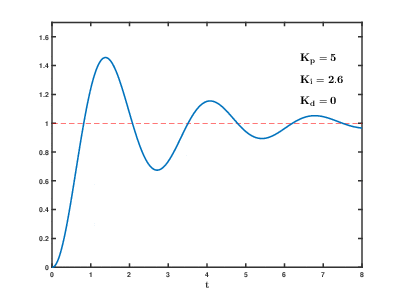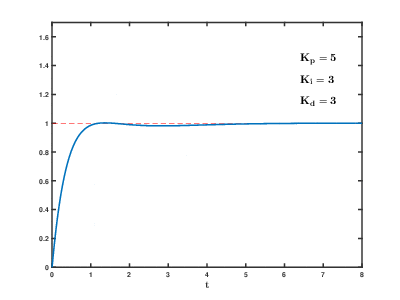
P제어
P : Proportion제어는 오차값만큼 제어량을 줍니다.
오차가 클수록 제어량이 크고, 오차가 적으면 제어량이 적죠.
pid제어에 가장 큰 역할을 하고 목표값에 도달하는 속도 역시 괜찮은 편이지만,
목표값에 가까워지면 더이상 목표값에 수렴하지 못하고 어느정도 오차가 있는 상태에서 더이상 제어가 되지 않습니다.
이를 잔류편차가 생긴다고 합니다.
PI제어
위의 P제어를 해결하기 위해 나온 제어방식이 Proportion 제어에 Integral-적분항을 추가해서 만든
PI제어인것이죠. PI제어는 오차의 비례값과 오차의 누적값을 제어량으로 사용해 P제어의 문제인 오차를 낮춥니다.
목표값에 정확히 수렴할 수 있도록 해주죠. 다만 이것도 문제가 있습니다.
도달하는데 시간이 너무 걸리고, 급격한 변화에 대응하기 어렵다는 것입니다.
PID제어
마찬가지로 PI제어의 단점을 보완할 제어로 PID제어가 등장합니다,
기존PI제어에 Derivative 미분항을 추가해 급격한 변화에도 대응하고, 도달시간을 줄일 수 있습니다.
위 내용은 사실 크게 중요하지는 않습니다. 그냥 pid=빠른 제어 라고만 생각해도 충분할테니까요.
다만 p, i, d 각각의 요소들이 제어기에 어떤 역할을하고, 어떤 영향을 미치는지 이해하는 데는
위 내용이 상당히 중요하게 다가올것이기 때문에 굳이 언급하게 되었습니다.
위 내용을 숙지하고 알고리즘을 보면
정체불명의 Kp, Ki, Kd가 있는 것을 보실겁니다.
위 값들은 pid 제어가 적절히 이루어지도록 하는 상수값으로, 적절히 맞췄을 때 최적의 성능을 냅니다.
그니까 우리가 노가다를 하며 세 값들은 모두 찾아야한다는 이야기죠.
어렵게 느낄 수 있겠지만 각 상수에는 자기들만의 성질이 있고, 그 성질을 힌트로 값을 찾아내면 됩니다.
Kp, p게인은 목표치에 가는 정도를 결정하는 상수입니다.
p게인이 너무 낮으면 목표값에 도달하기 어렵게됩니다. 제어량이 충분치 않기때문에 시간도 오래걸리고,
제어에 어려움을 겪기도 합니다.
반대로 p게인이 너무 높으면 제어량이 너무 커서 진동하기 시작합니다. 시소를 탄다고 하죠...
Ki, i게인은 목표치에 대한 정확도를 결정하는 상수입니다.
i게인이 너무 낮으면 위 설명처럼 목표치에 근접하기 어렵습니다.
반대로 i게인이 너무 높으면 시간이 오래걸리고, 외부 변화에 잘 대응하지 않습니다.
역동적인 움직임을 중시하는 드론 pid 게인값 설정에서는 특히 i게인 세팅이 중요하겠죠.
Kd, d게인은 목표치에 대한 속도를 결정하는 상수입니다.
d게인은 p게인으로 조금 부족한 제어량을 보충해주는 역할을 합니다.
순간 제어량을 확 높이면서 목표치에 도달하는 도움닫기 역할같은거죠.
d게인이 너무 낮으면 마찬가지로 시간이 오래걸리고, d게인이 너무 크면 진동이 생깁니다.
게인값에 따른 설명은 이정도 하겠습니다.
무엇보다 게인값에 따라 나타나는 진동의 종류와 차이를 직접 느끼는 것이 중요하다 생각합니다.
그 느낌을 파악하게 된다면 pid 게인값 찾는 것은 그리 어려운 일이 아닐 것입니다.